Exponents but Commutative

Commutative Tetration

Intro

Exponentiation is defined as repeated multiplication. So we might wonder why we don’t talk about repeated exponentiation; sometimes called tetration?

One reason repeated exponentiation is hard to talk about is that exponentiation is not commutative or associative. So repeating exponentiation means carefully tracking order and progress. If you tried to then repeat that operation, you’d have to specify which order you exponentiated in, then which order you tetrated in. There becomes exponentially many conventions for you to choose from.

We will discuss a binary operator that’s like exponentiation but commutative and associative. We’ll see how this can be used to define repeated exponentiation. And we’ll talk about a number of generalizations.

Recommended Background

Almost none needed.

Definition

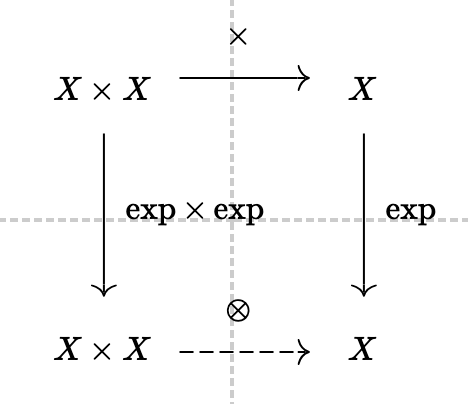
What do we mean by commutative exponentiation? Only exponentiation is exponentiation. But we mean a commutative / associative operator, ⊗, which distributes over multiplication, just like multiplication distributes over addition.

\(a\cdot(x+y)=ax+ay\)

\(a\otimes(x\cdot y)=a\otimes x\cdot a\otimes y\)

I’ll cut right to the chase. The operator that does this is:

\(x\otimes y = e^{\ln x\cdot \ln y}=x^{\ln y} = y^{\ln x}\)

That’s it. (Keep reading though!) You can check that these equalities are all the same. Let’s see why it distributes multiplication.

\(a\otimes(x\cdot y) = e^{\ln a\cdot\ln\left(xy\right)}=e^{\ln a\cdot\left(\ln x + \ln y\right)}=e^{\ln a\cdot\ln x + \ln a \cdot\ln y}=e^{\ln a\cdot\ln x}e^{\ln a \cdot\ln y}=(a\otimes x)\cdot(a\otimes y)\)

Notice how we were able to use the distribution property of multiplication over addition in the exponent, then use the fact that addition in the exponent becomes multiplication in the base.

In fact, it’s precisely the property of e^x, that it takes addition to multiplication that makes this all work. In the language of commutative diagrams, it may be helpful to picture this as the push-forward of multiplication along exp.

Note: We will only work with positive numbers for this.

Identity and Inverse

Like with multiplication, commutative exponentiation has an identity element and an inverse.

The identity element is e, because

\(x = x\otimes e = e\otimes x\)

Already this is nicer than exponentiation. Because although x^1=x, there is no identity element, c, for which c^x=x for all x.

The inverse of x is e^(1/ln x). Because:

\(x\otimes e^{1/\ln x} = e^{\ln x\ln e^{1/\ln x}}=e^{\ln x/\ln x} = e\)

and e is the identity element.

We can then define a inverse operator (comparable to division for multiplication:

\(x\oslash y = e^{\ln x/\ln y}\)

This allows you to solve equations:

\(x\otimes a=y\implies x=y\oslash a\)

Proto-Addition

Right now, we’re focusing on how we can go “up” continuing the progression of addition and multiplication. But you can also go “down,” finding an operator for which addition plays the role of multiplication and distributes over this new, lower operator.

\(a+(x\oplus y) = (a+x)\oplus(a+y)\)

This gets defined surprisingly similarly.

\(x\oplus y = \ln(e^x+e^y)\)

Notice that for both of our new operators, the operators get shoved in places that don’t reduce. If we had used multiplication here instead, then it would simplify to x+y.

This operator sorta has an identity element, -∞. And it has an inverse function that is sometimes well-defined:

\(x\ominus y = \ln(e^x-e^y)\)

Expontentiation

It might feel like we’ve lost something with this definition, because we no longer have a name for x*x*…*x (n times). But actually we can do this.

\(x^n=x\otimes e^n = x^{\cdot n}\)

The last part introduces a new syntax that will become useful later.

Notice the relationship

\(x^{\cdot n}=x\otimes(e\cdot e\cdots e)\)

with n unit elements multiplied.

Multiple Bases

Of course, the definition of “commutative exponentiation” isn’t the only one that meets the criteria of distributing over multiplication. The full family can be described by:

\(x\otimes_b y=x^{\log_by}\)

Different bases are related by

\(x\otimes_c y = x\otimes_b y \oslash_b e^\otimes_c = x^{\log_b y/\log_b c}=x^{\log_c y}\)

Where e_c^⊗ is the identity element of ⊗_c. the last equality follows from the change of basis formula.

It may surprise you that there are multiple choices for commutative exponential. But if you only require distributivity, then there are also multiple choices for “multiplication”.

\(x\cdot_b y = bxy =x\cdot_1 y\div_1 e^\cdot_b=x\cdot_1 y\div_1 \left(\frac{1}{b}\right)\)

Notice the identity element under “base-b multiplication” is 1/b, and not b.

There are no such “other base addition.” If there were, they’d have to be related under the relationship.

\(x+_by=x+_1y-e_1^+=x+_1y-(-\infty)\)

Tetration

Commutative repeated commutative exponentiation is called “commutative tetration.” We want to define it the same way we defined commutative exponentiation. Namely, we can define some new “exponential” function, called exp’ together with an inverse called log’. Then we can define a new binary operator as:

\(x\otimes'y = \exp'\left(\log'x\otimes\log'y\right)\)

This would be like the next operator up. And obviously, we could keep going in this direction. Now exp’ belongs to a family of functions that also includes discrete repeated commutative exponentiation. Say for example, apply ⊗ 4 times, so we could take exp’(x) = x ⊗ x ⊗ x ⊗ x.

Alternatively, we could look at the Taylor series for exp.

\(\exp (x) = 1+x/1+x^{\cdot2}/2/1 + x^{\cdot3}/3/2/1 + \cdots\)

If you compute exp(x)exp(y), distributing and combining like terms, you’ll find that you get exp(x+y).

\(\begin{array}{rcl} \exp (x)\cdot\exp(y) &=& (1+x/1+x^{\cdot2}/2/1 + \cdots)\cdot(1+y/1+y^{\cdot2}/2/1 + \cdots) \\ &=& (1) + (x/1+y/1) + (x^{\cdot2}/2/1+x\cdot y/1/1+y^{\cdot2}/2/1)+\cdots\\ &=&1 + (x+y)/1 + (x+y)^{\cdot 2}/2/1+\cdots\\ &=&\exp(x+y) \end{array}\)

Well, if instead we define:

\(\exp'(x) = e\cdot x\oslash e\cdot x^{\otimes2}\oslash e^2\oslash e\cdot x^{\otimes3}\oslash e^3\oslash e^2\oslash e\cdot\cdots\)

And you compute exp’(x)⊗exp’(y), then you’ll get

\(\begin{array}{rcl} \exp' (x)\otimes\exp'(y) &=& (e\cdot x\oslash e\cdot x^{\otimes2}\oslash e^2\oslash e \cdot \cdots)\otimes(e\cdot y\oslash e\cdot y^{\otimes2}\oslash e^2\oslash e \cdot \cdots) \\ &=& (e)\cdot (x\oslash e\cdot y\oslash e) \cdot (x^{\otimes2}\oslash e^2\oslash e\cdot x\otimes y\oslash e\oslash e\cdot y^{\otimes2}\oslash e^2\oslash e)\cdot\cdots\\ &=&e \cdot (x\cdot y)\oslash e \cdot (x\cdot y)^{\otimes 2}\oslash e^2\oslash e+\cdots\\ &=&\exp'(x\cdot y) \end{array}\)

by the exact same math.¹

Because it satisfies this property, we can use exp’ in a commutative diagram, similar to how we defined above. This implicitly defines commutative tetration.

Using this same general structure, you can go “up” or “down” operators forever.

Conclusions and Other Things to Think About

We introduced some new ideas and thoughts relatively quickly, and you may be thinking about lots of things. I’ve found the follow threads to be the most promising to pull on.

1. Domain expansion. Complex numbers were discovered² as solutions to exponent problems. It seems that each new operator we create here presents new solutionless problems, and one wonders if we should try to name and study these. Log branches on complex numbers almost offers a way out, but it doesn’t lead to a complete answer.

2. Metacalculus.³ If you view derivatives as differences and integrals as weighted averages, you can ask what this looks like if we shift the operators up or down. The result gets you product integrals⁴ and other peculiar operations.

3. Ring theory. Because you can repeat this work for abstract rings, you can give additional structure to the ring of your choice. This seems to cast the discrete log problem⁵ in a new light.

1. We take for granted that this converges.

2. Or invented

3. Metacalculus has been well-studied.

4. Product intervals has been found to solve a few difficult calculus problems.

5. The discrete log problem states that calculating discrete logs is generally computationally expensive. An efficient algorithm would prove that P=NP.